
#10. 결정 트리
결정 트리
결정 트리 모델
- 루트 노드 → 결정 노드 → 리프 노드
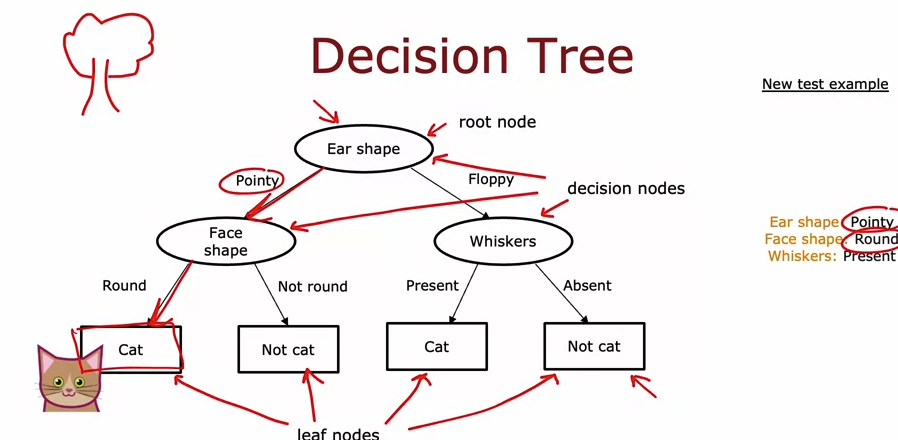
배우는 과정
1⃣ 결정 1: 각 노드에서 침을 뱉을 피처를 선택하는 방법
- 순도 최대화(또는 불순물 최소화): 가능하면 결과 값에 하나의 클래스만 나타나도록
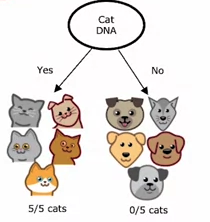
2⃣ 결정 2: 언제 헤어짐을 멈출 것인가?
- 매듭이 있는 경우 100% 한 수업
- 노드를 분할하면 트리가 생성됩니다. 최대 깊이 초과(설정값)
- 개선된다면 순도 문턱 이하이다
- 만약에 노드의 인스턴스 수 임계값 미만
의사 결정 트리를 배우십시오
순도 측정
불순물의 척도로서의 엔트로피
- 엔트로피 차트: p1의 값으로 순도를 확인할 수 있음(P1이 0 또는 1에 가까울수록 엔트로피는 0이 됨)
- H(p1) = -p1 * log2(p1) – p0*log2(p0) = -p1 * log2(p1) – (1-p1) * log2(1-p1) ※ p0 = 1-p1
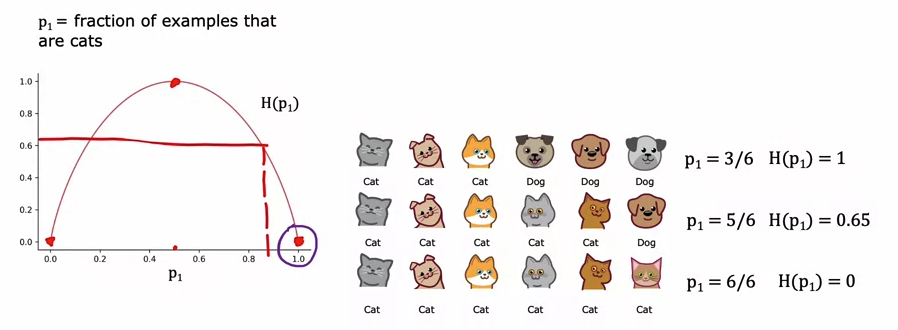
스플릿 선택 : 정보 획득
정보 이득: 루트 노드의 엔트로피에서 샘플 수에 엔트로피를 곱하고 가중치를 곱한 값을 빼서 분할 옵션을 선택합니다.
- 루트 노드: 고양이 5마리와 개 5마리이므로 p1 = 0.5, H(0.5) = 1
- ‘얼마나 줄였는가’의 차이를 봤기 때문에 엔트로피 값이 결과이므로 해당 값이 가장 큰 것이 = 선택한 값
- 따라서 아래 예에서 0.28은 가장 많이 줄어들기 때문에 선택한 분할입니다.
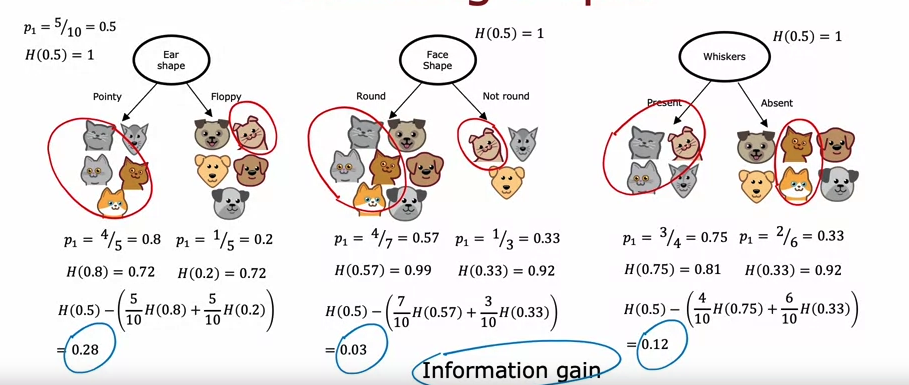
- w = 숫자, p = 고양이 확률

조립
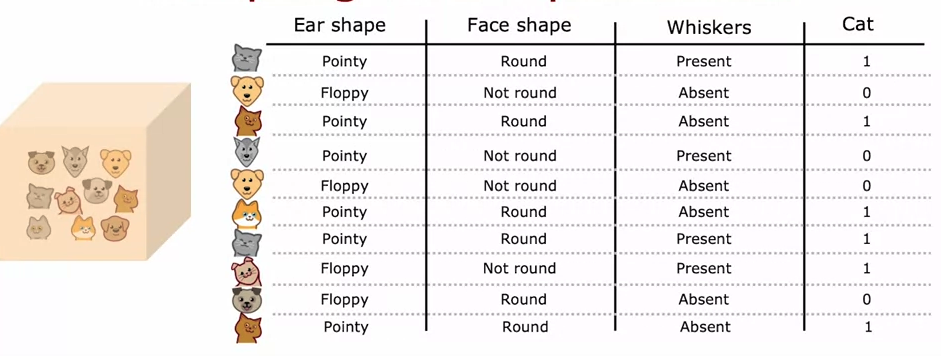
의사 결정 트리 학습 방법
- 1. 모든 샘플을 루트 노드에 놓고 시작
- 2. 가능한 모든 특성에 대한 정보 이득을 계산한 후 값이 가장 높은 특성을 선택합니다.
- 3. 기능별로 레코드를 분리하고 계속 분할
- 4. 다음 기준이 충족되면 분할을 중지합니다.
- 4.1 노드가 100% 클래스가 되는 경우(분류)
- 4.2 설정된 최대 깊이에 도달했을 때
- 4.3 정보 획득량이 설정한 기준치 이하인 경우
- 4.4 노드의 샘플 수가 설정된 임계값보다 작아지는 경우
범주형 특성의 원-핫 코딩 사용
- 3개 이상의 특성으로 노드를 구성해야 하는 경우 원-핫 인코딩을 사용하여 이진 특성으로 만들어야 합니다.
- 예: 귀 모양이 1) 뾰족한지 2) 접힌지 3) 둥글다면 feature는 1) 뾰족한지 여부 2) 접힌지 여부 3) 둥글지 않은지 여부로 변환하여 0, 1을 반환합니다.
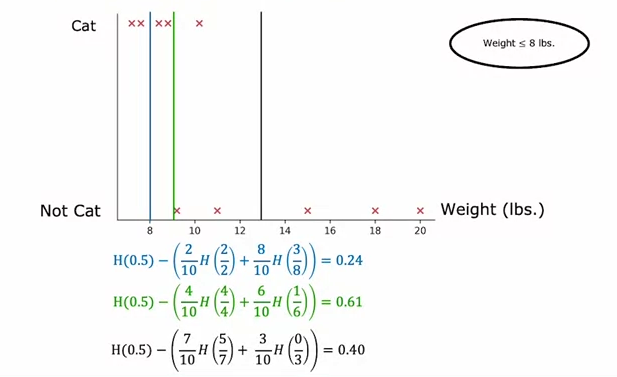
지속적으로 높이 평가되는 속성
- 연속 변수를 사용하려면 변수를 임계값으로 설정하고 이진 특성으로 만들어야 합니다.
- 기준점은 정보 이득을 사용하여 가장 높은 기준을 선택합니다(10개의 샘플로 9번 시도해야 하며, 이는 나눌 수 있는 기준입니다).
회귀 트리
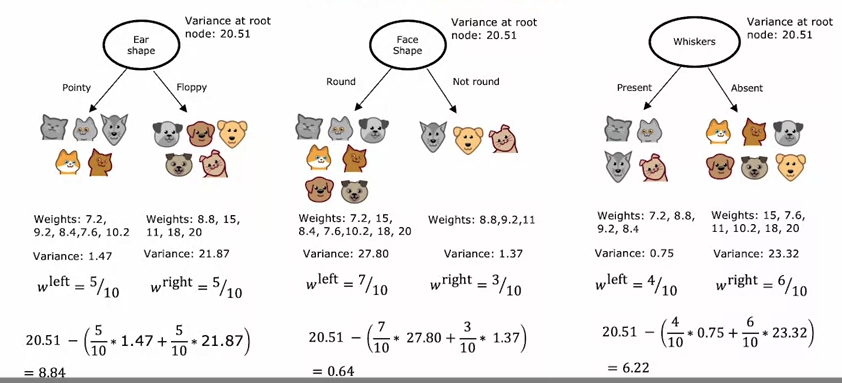
회귀 트리는 회귀(예측 수)에도 사용할 수 있습니다.
스플릿에서
모든 샘플의 분산 – {각 기능 분류의 (분산 값 * 샘플 수)의 합계} 가장 높은 것을 선택합니다.
분산을 가장 많이 줄이는 옵션을 선택하려면
#1. 엔트로피 계산식
def entropy(p):
if p == 0 or p == 1:
return 0
else:
return -p * np.log2(p) - (1- p)*np.log2(1 - p)
#2. Split
def split_indices(X, index_feature):
"""Given a dataset and a index feature, return two lists for the two split nodes, the left node has the animals that have
that feature = 1 and the right node those that have the feature = 0
index feature = 0 => ear shape
index feature = 1 => face shape
index feature = 2 => whiskers
"""
left_indices = ()
right_indices = ()
for i,x in enumerate(X): #인덱스와 원소로 이루어진 튜플(tuple)반환
if x(index_feature) == 1:
left_indices.append(i)
else:
right_indices.append(i)
return left_indices, right_indices
#3. Weighted entropy
def weighted_entropy(X,y,left_indices,right_indices):
"""
This function takes the splitted dataset, the indices we chose to split and returns the weighted entropy.
"""
w_left = len(left_indices)/len(X)
w_right = len(right_indices)/len(X)
p_left = sum(y(left_indices))/len(left_indices)
p_right = sum(y(right_indices))/len(right_indices)
weighted_entropy = w_left * entropy(p_left) + w_right * entropy(p_right)
return weighted_entropy
#4. Information gain
def information_gain(X, y, left_indices, right_indices):
"""
Here, X has the elements in the node and y is theirs respectives classes
"""
p_node = sum(y)/len(y)
h_node = entropy(p_node)
w_entropy = weighted_entropy(X,y,left_indices,right_indices)
return h_node - w_entropy
#Computing
for i, feature_name in enumerate(('Ear Shape', 'Face Shape', 'Whiskers')):
left_indices, right_indices = split_indices(X_train, i)
i_gain = information_gain(X_train, y_train, left_indices, right_indices)
print(f"Feature: {feature_name}, information gain if we split the root node using this feature: {i_gain:.2f}")
나무 앙상블
다중 결정 트리 사용
트리가 하나만 있는 경우 데이터를 변경하면 완전히 다른 트리가 생성될 수 있습니다.
따라서 새로운 데이터가 도착하는 시점을 대다수가 결정할 수 있도록 여러 개의 트리 앙상블이 생성됩니다.
교체로 샘플링
새로운 훈련 세트: 데이터 세트에서 임의 샘플링으로 여러 데이터 세트 저장(중복 데이터 선택 가능!)
랜덤 포레스트 알고리즘
트리 샘플 생성
새로운 트레이닝 세트로 의사 결정 트리 구축 * 각각의 새로운 데이터 세트에 대해(B회 반복)
B 값이 높을수록 좋지만 100을 넘으면 성능이 크게 향상되지 않습니다.
기능 선택의 무작위화
각 노드에서 분할에 사용할 기능을 선택할 때 N 기능을 사용할 수 있는 경우 임의의 하위 집합을 선택합니다. 케이 (
즉, 훈련 샘플에 포함될 특징의 수(k)는 전체 특징의 수(n)보다 작게 선택되며 일반적으로 n의 제곱근을 취합니다.
XGBoost
나무의 직감 향상
트리를 여러 번 구축할 때 훈련 데이터셋에서 샘플링할 때 샘플링은 랜덤이지만, 기존 트리가 잘 분류하지 못한 원본 데이터셋의 샘플 데이터에 포함시켜 트리 모델의 성능을 향상시킨다.
XGBoost(eXtreme Gradient Boosting)
#Classification
from xgboost import XGBClassifier
model = XGBClassifier()
model.fit(X_train,Y_train)
model.predict(X_test)
#Regression
from xgboost import XGBRegressor
model = XGBRegressor()
model.fit(X_train,Y_train)
model.predict(X_test)
